在机器学习常用的回归模型中，我们使用预测变量(predictors)的线性组合来预测感兴趣的变量，而在自回归模型(autoregression)模型中，我们某个变量过去的取值来预测这个变量。所以这里自回归表示用自己预测自己。而与自回归模型不同，移动平均模型(moving average model)是以类似回归的形式使用过去的预测误差进行预测。

1. Autoregressive models

则自回归模型可以表示成如下形式：
$$
y_t=c+\phi_1y_{t-1}+\phi_2y_{t-2}+ \ldots + \phi_py_{t-p}+\epsilon_t
$$
这里$\epsilon_t$表示白噪声，我们把上述模型叫做一个$p$阶的自回归模型，可以表示为AR(p) model。
自回归模型可以极其灵活的处理很多种不同的时间序列模式。如下图所示展示了AR(1)模型和AR(2)模型。通过改变参数$\phi_1,\ldots,\phi_p$可以产生不同的时间序列模型，而误差项$\epsilon_t$只会影响序列的尺度，不会影响patterns。



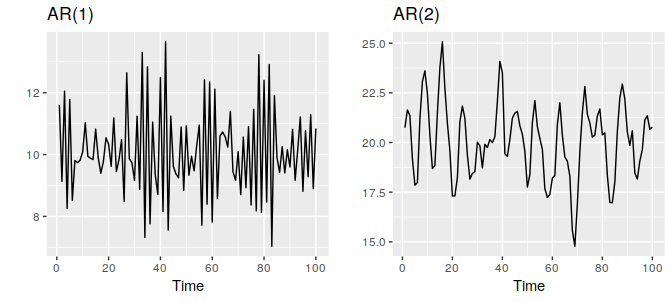
上面两个图中，第一个AR(1)模型和第二个AR(2)模型的函数分别为：
$$
\begin{aligned}
AR(1):\quad y_t & = 18-0.8y_{t-1}+\epsilon_t \\
AR(2):\quad y_t & = 8+1.3y_{t-1}-0.7y_{t-2}+\epsilon_t
\end{aligned}
$$
对于AR(1)模型：

  • 当$\phi_1=0$的时候，$y_t$等价于白噪声(white noise)
  • 当$\phi_1=1 \ \land \ c=0$的时候，$y_t$相当于随机游走(random walk)
  • 当$\phi_1=1 \ \land \ c\neq0$的时候，，$y_t$相当于带有漂移的随机游走(random walk with drift)
  • 当$\phi_1<0$的时候，$y_t$会在均值附近震荡(oscillate)

一般来说，为了约束自回归模型为stationary数据，我们可以约束自回归模型的参数。

  • 对于AR(1)模型：$-1<\phi_1<1$
  • 对于AR(2)模型：$-1<\phi_2<1,\phi_1+\phi_2<1,\phi_2-\phi_1<1$

当$p\geq3$的时候，约束就会变得很复杂了。

2. Moving average models

移动平均模型的形式如下：
$$
y_t=c+\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\ldots+\theta_q\epsilon_{t-q}
$$
这里$\epsilon_t$是白噪声，我们把这个模型叫做q阶的MA(q)模型，当然我们其实无法观测到变量$\epsilon_t$的取值，所以它不算是通常意义上的回归模型。它知识认为$y_t$的值可以由过去的预测误差值的加权移动平均得到。如下图展示了两个模型MA(1)和MA(2)。



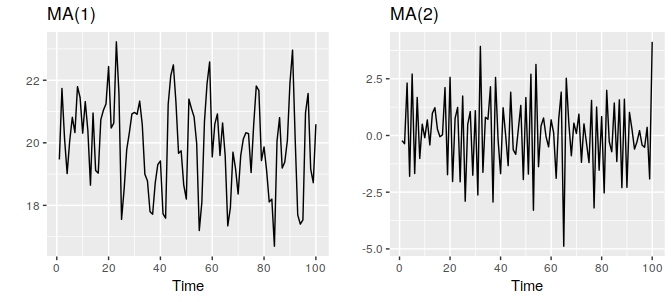
上图中的两个模型MA(1)和MA(2)分别为:
$$
\begin{aligned}
MA(1): \quad y_t &= 20+\epsilon_t+0.8\epsilon_{t-1} \\
MA(2): \quad y_t &= \epsilon_t - \epsilon_{t-1} + 0.8\epsilon_{t-2}
\end{aligned}
$$
其实任何一个stationary $\text{AR}(p)$模型都可以表示成一个$\text{MA}(\infty)$模型，我们可以推到以下AR(1)模型。
$$
\begin{aligned}
MA(1): \quad y_t &= \phi_1y_{t-1}+\epsilon_t \\
&= \phi_1(\phi_1y_{t-2}+\epsilon_{t-1})+\epsilon_t \\
&= \phi_1^2y_{t-2}+\phi_1\epsilon_{t-1}+\epsilon_t \\
&= \phi_1^3y_{t-3}+\phi_1^2\epsilon_{t-2}+\phi_1\epsilon_{t-1}+\epsilon_t \\
&= etc.
\end{aligned}
$$
如果$-1<\phi_1<1$，随着$k$变大，$\phi_1^k$的值会越变越小，最终我们得到如下公式。
$$
y_t=\epsilon_t+\phi_1\epsilon_{t-1}+\phi_1^2\epsilon_{t-2}+\phi_1^3\epsilon_{t-3}+\ldots
$$
即为一个$\text{MA}(\infty)$模型。如果里面的参数$\phi_1$和$\phi_2$有满足上面提到的约束，则这个MA模型是可逆的，它可以转化为一个AR模型，也就是我们可以将任何可逆的MA(q)模型，转化成$\text{AR}(\infty$)模型，而且我们不仅仅是为了转化，这个过此中也有一些很不错的数学性质。比如我们将一个MA(1)过程，$y_t=\epsilon_t+\theta_1\epsilon_{t-1}$转化成它的相应$\text{AR}(\infty)$模型,则有如下性质：
$$
\epsilon_t=\sum_{k=0}^\infty(-\theta)^jy_{t-j}
$$
此处未完待续…